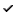3D Matrix

If you are familiar with matrices in 3d graphics and OpenGL in particular you may skip this topic to the end.

Basics

Here is basic and naive explanation of matrices in 3d graphics. It may be not mathematically correct, but it should enough to understand what is this and how to work with them.

Matrix defines local coordinate system or transformation. Local coordinate system means position and orientation of object in 3d space. Transformation may contain rotation, scale, shear and position.

All these transformations are encoded in matrix. Multiplying vector by matrix gives transformed vector. Multiplying matrix by matrix gives new transformation.

1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1

Matrix is square table of 4x4 numbers. This is an identity matrix - matrix without transformations. Last column is always 0,0,0,1 and matrices quite often are stored as 3x4 Actually last column may be used for perspective transformation, which is very internal stuff.

Green part defines rotation and scaling. Last row (yellow part) defines position. Each row in green part is an axis of local coordinate system.

Position is quite easy to see, it contains non encoded XYZ coordinate.

If you will take a look at raw numbers in matrix it is possible to see what kind of transformations it contains.

1	0	0	0
0	1	0	0
0	0	1	0
10	20	30	1

If last row is non zero - translation is present. On image above translation is 10 by X, 20 by Y and 30 by Z.

If 3x3 part is non identity, then it has rotations and possibly scaling.We even may try to understand what kind of transformation encoded in 3x3 part.

Transformation of point work in the following way:

where m - matrix, a - original point, b - transformed point

Transoformation of vector:

As you may see, difference is only in using translation component. With such equation point/vector transformed from local coordinate system to world system. Or just transformed.

If we want to combine transformation of two matrices we should multiply them.

For instance if we want to transform point from objb to world we may transform it by matrix of objb object, after that transform it by matrix of obja. Alternativelly we may construct composed matrix : tm = tmb*tma and transform point with this new matrix.

 

Inverse matrix - this is opposite to original matrix. It transforms point from world to local system. Usually there is a function which generates inverse matrix from given one.

How to define transformation in matrix.

We may write numbers directly, but this is reasonable only in case if we know axes of local coordinate system. If we want to use rotations, scaling and translation, we should use much simple methods:

• Rotate around X or Y or Z axis,
• Rotate around any axis defined XYZ component.
• Scale by X,Y,Z. Axis.
• Translate by X,Y,Z
• Move to X,Y,Z.

By incrementally applying such operations we may define any transformation. Order is important. Usually we do: Scale, Rotation, Position (PRS).

WebGL

In webgl matrices are represented via array of 16 numbers.

0	1	2	3
4	5	6	7
8	9	10	11
12	13	14	15

 It may be constructed as var tm=[] or in case of node: var tm=node.enableTM(true); This method returns or creates current matrix. If matrix was just created it is identity matrix. After that you may apply transformations, this will move objects to new position.

Methods

mat4 is global namespace for matrix functions. They operates on array of 16 numbers - matrix.

We have to be very efficient in JavaScript, that's why these methods are low level and not very friendly. If you neeed more functions, please contact us.

mat4.identity(m)

Methos makes an identity matrix.

m	Matrix. Array of 16 numbers.

Method returns matrix.

mat4.offset(m,a)

Relativelly tranlates matrix

m	Matrix to modify.
a	Offset. This argument is an array of 3 numbers

mat4.setScale(m,a)

Method sets uniform scaling in identity matrix.

m	Matrix to modify.
a	Scale.

mat4.rotateAxisOrg(m,axis,org,angle)

Method rotates matrix around axis with defined origin by specified angle

m	Matrix to modify.
axis	Axis of rotation
org	Any point on line of rotation
angle	Angle in radians

mat4.mulPoint(m,src,dst)

Method transform point by matrix.

m	Transformation matrix .
src	Source point. Array of 3 numbers.
dst	Destination point. If not specified, source point will contain transformed result.

Method returns transformed point.

mat4.mulVector(m,src,dst)

Method transform point by matrix.

m	Transformation matrix .
src	Source vector. Array of 3 numbers.
dst	Destination vector. If not specified, source point will contain transformed result.

Method return transformed vector.

mat4.m(a,b,c)

Method multiples a and b matrices.

c=b*a	c is defined.
b=b*a	c is not defined

Method returns resulted matrix.

mat.invert(out,m)

Method computes inverted matrix.

out	Output array for resulted matrix
m	Source matrix